Статистическая гипотеза - это предположение о виде распределения и свойствах случайной величины (генеральной совокупности), которое можно проверить (подтвердить или опровергнуть) статистическими методами на основе имеющейся выборки.
В определении статистической гипотезы содержатся все свойства и границы применения этого понятия. Не является статистической гипотеза о том лжёт ли человек или говорит правду, отвечая на вопросы.
Статистические гипотезы могут быть поставлены непосредственно практикой, так и выдвинуты в результате первичного анализа данных.

Примеры наиболее распространённых статистических гипотез:

1) О равенстве математических ожиданий 2-х генеральных совокупностей;
2) О равенстве дисперсий нескольких генеральных совокупностей;
3) Об однородности двух выборок (о том, что обе выборки взяты из одной генеральной совокупности);
4) О наличии аномальных результатов наблюдений (выбросов);
5) О независимости двух случайных величин.

Статистическая гипотеза всегда формулируется в виде двух противоположных предположений: нулевой гипотезы (Н ₀) и противоположной ей (Н₁). Нулевая гипотеза является основной и принимается верной по умолчанию,
если нельзя доказать обратного. Формулировка альтернативной гипотезы зависит от практической задачи.

Статистикой называется некоторая функция от выборочных данных. Например, выборочное среднее является статистикой. Так как статистика это функция выборочных данных - случайных величин, то она сама является случайной величиной. Правило проверки статистической гипотезы при некоторой фиксированной альтернативе называется статистическим критерием. Статистика по которой судят о справедливости статистической гипотезы называется статистикой критерия и как правило обозначают буквой - Z.

Уровень значимости alpha - столь маленькая вероятность, что событие с такой вероятностью принимается практически невозможным. На практике используют следующие уровни значимости: 0.001, 0.01, 0.05, 0.1.
Критической областью критерия называется подобласть области значения статистики критерия, вероятность попадания в которую для этой статистики, при условии истинности H ₀, равна уровню значимости, т.е. принимается как практически невозможное событие.

Пример правосторонней критической области:

Статистическая гипотеза

Общая схема проверки статистической гипотезы.

1) Формулируют H ₀ и H₁;
2) Выбирают уровень значимости;
3) Выбирают критерий и статсистику критерия;
4) Строят критическую область при условии справедливости H ₀;
5) Вычисляют выборочное значение Z;
6) Проверяют принадлежит ли выборочное значение Z критической области;
7) Если принадлежит - принимают, что H ₀ неверна на выбранном уровне значимости, в противном случае принимают, что H₀ верна.

Пусть статистика критерия Z, имеет некоторую функцию распределения при условии истинности H ₀. По данным полученной выборки находят значение Z.

p - значением (p - value) называется вероятность того, что статистика критерия примет значение такое же как наблюдаемое Z или более "экстремальное" (большее, либо меньшее) при условии, что верна нулевая гипотеза.

Пример правостороннего критерия:

Чем большее значение, наблюдаемое в ходе опыта, принимает Z тем менее вероятно, что справедлива Н₀.

Схема проверки статистической гипотезы с использованием p - value.

1) Формулируют H₀ и H₁;
2) Выбирают уровень значимости;
3) Выбирают критерий и статсистику критерия;
4) Вычисляют выборочное значение статистического критерия;
5) Вычисляют значение p - value;
6) Сравнивают p - value с уровнем значимости alpha;
7) Принимают решение. Если p - value > alpha, то оставляют верной H₀. Если p - value < alpha то H₀ отвергают и принимают верной H₁.

Параметрические методы статистики основаны на знание общего вида вероятностного распределения случайной величины, описывающей генеральную совокупность. Допустим может быть известно, что данные наблюдений получены из нормального распределения с неизвестным матожиданием, гипотезу относительно которого необходимо проверит. В этом случае могут быть использованы статистики закон распределения которых зависит от распределения исходной случайной величины. Например, закон распределения среднего выборочного значения зависит от параметров исходной генеральной совокупности.
На практике закон распределения исходной генеральной совокупности, как правило, неизвестен и использование параметрических методов статистики может приводить к
ошибкам существенно и непредсказуемо превышающими ожидаемые, и поэтому является необоснованным.

Физиологические параметры, регистрируемые в ходе опроса на полиграфе, имеют неизвестное вероятностное распределение. Выдвинуть и проверить гипотезу относительно их распределения в силу малости выборки является малоперспективным действием.
Критерий называется непараметрическим, если закон распределения критерия не зависит от закона распределения генеральной совокупности. В этом смысле можно сказать, что непараметрические методы статистики являются свободными от распределения. Они не полагаются на допущения о том из какого вероятностного распределения получена выборка. Порядковая статистика, основанная на рангах наблюдений, является примером статистики независящей от параметров конкретных распределений. Она играет главную роль в тестах, которые используются в данной программе.

Критерий знаковых ранговых сумм Вилкоксона

оКритерий знаков не использует значительную часть информации, содержащейся в выборке. Например, он учитывает «направления» различия амплитуды КГР, но не учитывает относительные размеры этих разностей. В случае опроса на полиграфе не равноценными являются ситуации, когда амплитуда КГР на проверочный вопрос превосходит амплитуду КГР на вопрос сравнения на 5%, с той, когда превосходит на 50%.
В значительной мере этого недостатка лишён критерий знаковых ранговых сумм Вилкоксона (Уилкоксона). В этом тесте все наблюдаемые разности случайных величин ранжируются без учёта их знака (например, амплитуд КГР). Затем составляются две статистики:

V ₊ = сумма рангов положительных разностей
V _- = сумма рангов отрицательных разностей

Если выполняется H _0, то необходимо ожидать, эти статистики будут примерно одинаковы. Тогда как при справедливости H₁ одна из сумм будет значимо превосходить другую. На практике за статистику критерия выбирают меньшую сумму (при этом вторая определяется однозначно).

Если статистика критерия достаточно мала, то делается выбор в пользу H₁, иначе признаётся, что в результате теста не получено достаточных оснований для отклонения H₁.
В случае опроса на полиграфе H ₀ соответствует ситуации так называемой «неопределённости», когда не получено данных для принятия конкретного решения. А H₁ - реакции на проверочные и сравнительные стимулы различаются статистически значимо, и полиграфолог имеет достаточно оснований для принятия решения.
Необходимо помнить, что, например, p – value не является ни вероятностью правдивости/лживости опрашиваемо, ни вероятностью ошибки при принятии решения полиграфологом. В контексте опроса на полиграфе p – value следует рассматривать только как критерий для принятия решения полиграфологом.

В случае, когда в результате одного опыта/наблюдения измеряются две случайных величины (случайная величина – это величина точное значение, которой невозможно предсказать до измерения) ставится вопрос о корреляции измеряемых переменных. Понятие корреляции отражает их статистическую взаимосвязь, которая может быть как положительной, так и отрицательной. Например, рост и вес людей являются случайными величинами, между которыми имеется положительная статистическая зависимость. Хоть мы и не можем заранее сказать, какой рост и вес будет у конкретного случайного образом взятого человека, но может с большой уверенностью предсказать, что чем выше будет человек тем больше будет у него вес. Конечно, это правило будет выполнятся в среднем, для некоторой конкретной пары людей может оказаться, что дело обстоит обратным образом, но для достаточно большого количества случайно отобранных людей эта статистическая зависимость будет подтверждаться с большой долей вероятности.

Для того, чтобы наглядным образом обнаружить корреляцию строят так называемые диаграммы рассеяния. В случае двух переменных – это координатная плоскость. Для указанного примера по оси абцис можно отложить вес, а по оси ординат рост.

Точки – это рост и вес конкретного человека. По характеру расположения точек можно видеть, что статистическая связь между ростом и весом имеет линейный характер. Связь эта положительная, с увеличением массы увеличивается и рост. Прямая линия – это выборочная линия регрессии, построенная методом МНК (метод наименьших квадратов). Она наглядным образом показывает характер статистической зависимости двух случайных переменных. Её уравнение, которое называют выборочным уравнением регрессии y на x – это уравнение зависимости условного среднего от x вида:

Условным средним называют среднее арифметическое наблюдавшихся значений y, соответствующих x = x_0, где x₀ некоторое конкретное значение x. Например, если при x = 5 игрек принимала значения: 5,10,15, то

В том случае, когда между переменными отсутствует статистическая связь коэффициент k (коэффициент регрессии) перед переменной x равен нулю. При этом диаграмма рассеяния и прямая регрессии имеют следующий вид.

С коэффициентом k связан выборочный коэффициент линейной корреляции Пирсона

Его значения принадлежат отрезку [-1,1]. Близость его к -1 говорит о сильной отрицательной корреляции, близость к 1 – о сильной положительной. Обычно о сильной корреляции говорят, если коэффициент корреляции по модулю более 0,7. Если он близок к нули,то переменные не имеют статистической связи.

Так как выборочный коэффициент корреляции Пирсона вычисляется на выборочных (случайных) данных, то он сам является случайной величиной. Поэтому возникает вопрос о том, насколько статистически значимо полученное значение отличается от нуля, а значит переменные имеют статистическую связь и значимо полученное уравнение регрессии. В этом случае имеются прямая и альтернативная статистическая гипотезы:

Расчёт p – value для проверки H₀ производится посредством t – критерия Пирсона.
Условия применения выборочного коэффициента корреляции Пирсона:
1. Переменные должны быть из совместного нормального распределения;
2. Между переменными должна быть линейная взаимосвязь;
3. В выборке должны отсутствовать выбросы.

Если две случайные величины независимы, то их коэффициент корреляции всегда равен нулю. Обратное, вообще говоря, не верно.

Статистическая зависимость двух случайных величин не всегда означает, что они связаны причинно – следственной связью, т.е. не обязательно одна влияет на другую. Может присутствовать третья переменная, которая оказывает влияние на две первые. Именно, значение этой третьей переменную и пытается установить полиграфолог, измеряя изменение физиологических параметров человека. Она является качественной и принимает два значения: правдив человек или нет. Ситуация, когда одна переменная оказывает прямое влияние на вторую, полиграфологом должна отмечаться как «артефакт». Например, если глубокий вздох вызывает изменения в КГР, то такой вопрос должен быть исключён из анализа. Другими словами, между физиологическими параметрами, измеряемыми датчиками полиграфа, не должна присутствовать причинно – следственная связь.

Если не выполняются условия для применения выборочного коэффициента Пирсона, то применяются его непараметрические аналоги: коэффициент корреляции Спирмена и коэффициент корреляции Кэндалла. Оба метода переходят от реальных значений переменных к их рангам. Также они используются, когда переменные (одна или обе) измерены в порядковой шкале.

Пусть X ₁, X₂, … X_n – это разности амплитуд КГР на проверочные и вопросы сравнения
Y ₁, Y_2, … Y_n – это разности длин волн дыхания.

Тогда R_1, R_{2, …} R_n и S₁, S₂, … S_n – соответствующие им ранги.
Коэффициент ранговой корреляция Спирмена вычисляется по формуле

При выполнении гипотезы H₀ о независимости случайных величин математическое ожидание к.р.к. равно нулю . Альтернативная гипотеза H₁ – случайные переменные зависимы.

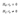
Коэффициент ранговой корреляции Кэндалла

Основан на сравнении доли согласованных пар и несогласованных. Пару наблюдений (значений двух случайных величин зафиксированных в двух наблюдениях) называют согласованной, если порядок следования рангов обоих случайных величин совпадает.
В противном случае пара называется несогласованной.

Пусть C – число согласованных пар, D – число несогласованных, тогда коэффициент ранговой корреляции Кэндалла вычисляется по следующей формуле:

Фактически обладает теми же свойствами, что и к. р. к. Спирмена

Оба коэффициента Кэндалла показывают наличие монотонной взаимосвязи между признаками, а не только линейной как к. к. Пирсона. В случае наличия монотонной связи к.р.к Кэндалла, как правило, принимает меньшие значения чем Спирмена.

Если количество признаков переменных больше двух, то в результате ранжировки имеют дело с несколькими последовательностями рангов. В программе – это три последовательности рангов, соответствующие дыханию, КГР и кардиоканалу. Для проверки хорошо ли согласуются эти ранжировки друг с другом используют коэффициент конкордации Кэндалла.

Где

– сумма рангов присвоенных i - му

элементу выборки по каждой из переменных, минус среднее значение этих сумм рангов (например, сумма рангов по каналам КГР, дыхания, кардио для i – го проверочного вопроса). m – число переменных/признаков, n – объём выборки. В программе m = 3, а объём выборки – это количество пар сравниваемых вопросов. Коэффициент конкордации Кэндалла принимает значения на отрезке [0,1]. Ноль соответствует полной рассогласованности рангов, единица полной согласованности. На практике при значении более 0,7 говорят о высокой степени согласованности ранжировок. Коэффициент конкордации рассматривают как показатель согласованности, тесноты связи между признаками/переменными и используют для проверки гипотезы H₀ - о независимости совокупности признаков/переменных. Для оценки значимости коэффициента конкордации вычисляют p – value. При его значении меньшем 0,05 W признают статистически значимым на уровне alpha = 0,05. Коэффициент конкордации имеет связь с коэффициентом ранговой корреляции Спирмена. Среднее арифметическое к. р. к. Спирмена всех пар переменных/признаков равно

В случае опроса на полиграфе m = 3 и

Высокая степень согласованности всех трёх физиологических параметров может свидетельствовать о действии ненаблюдаемой переменной, влияющей на физиологические параметры (лживость/правдивость), и является достаточным (но не необходимым) основанием для принятия решения полиграфологом. При наличии сильной корреляции между дыханием и КГР, дыханием и кардио следует обратить на возможность скрытого противодействия и дополнительных признаков, которые подтверждали бы эту возможность.